Number of Ways to Reorder Array to Get Same BST

update Nov 22, 2020

leetcode

Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.

For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.

Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.

Since the answer may be very large, return it modulo 10^9 + 7.

Example 1

Input: nums = [2,1,3]
Output: 1
Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.

Example 2

Input: nums = [3,4,5,1,2]
Output: 5
Explanation: The following 5 arrays will yield the same BST: 
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
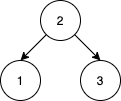
[3,4,1,2,5]
[3,4,1,5,2]

Example 3

Input: nums = [1,2,3]
Output: 0
Explanation: There are no other orderings of nums that will yield the same BST.

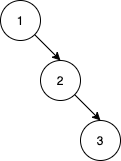
Example 4

Input: nums = [3,1,2,5,4,6]
Output: 19

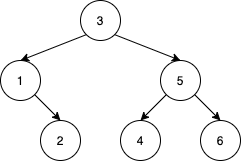
Example 5

Input: nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18]
Output: 216212978
Explanation: The number of ways to reorder nums to get the same BST is 3216212999. Taking this number modulo 10^9 + 7 gives 216212978.

Constraints:

1. 1 <= nums.length <= 1000
2. 1 <= nums[i] <= nums.length
3. All integers in nums are distinct.

Basic Idea:

这道题很有意思，首先我们通过观察发现对于一棵BST，输入数组的第一个数字是root，其后所有属于左子树的元素和所有属于右子树的元素在保证内部顺序不变的情况下是可以互相交换位置的，例如example4 中 1 和 5 的顺序可以交换，而且只要保证相对顺序，[1,2], [5,4,6]的顺序也可以交换。于是我们就得到了一种计算方法，即总的排列个数等于左右子树保持内部顺序不变互相交换位置的排列次数与左右子树内部所有可能的排列次数相乘。

注意到上面的算法需要考虑一个子问题，即两个有序数组在保证内部顺序不变的情况向合并为一个数组共有多少种方法，答案是 C(m+n, m) 或 C(m+n, n)，想象为一共有m+n个空格，选择m个插入数组A，剩下的插入数组B。

我们注意到这些组合数实际上形成了杨辉三角形，可以通过DP提前计算。

Java Code:

class Solution {
    private static int MOD = (int) 1e9 + 7;
    private int[][] dp = new int[1001][1001];
    public int numOfWays(int[] nums) {
        init();
        List list = Arrays.stream(nums).boxed().collect(Collectors.toList());
        return (int) dfs(list) - 1;
    }

    private long dfs(List<Integer> nums) {
        if (nums.size() <= 1) return 1;
        int first = -1;
        List<Integer> left = new ArrayList<>(), right = new ArrayList<>();
        for (int num : nums) {
            if (first == -1) first = num;
            else if (num < first) left.add(num);
            else right.add(num);
        }
        return (long) dp[left.size() + right.size()][left.size()] * dfs(left) % MOD * dfs(right) % MOD;
    }

    private void init() {
        for (int i = 0; i < dp.length; ++i) {
            for (int j = 0; j <= i; ++j) {
                if (i == 0 || j == 0) dp[i][j] = 1;
                else dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % MOD;
            }
        }
    }
}